专题3 圆的基本性质
题型一 点与圆的位置关系
例 1 [2017·大冶校级月考]若⊙O 的半径为5 cm ,平面上有一点A ,OA =6 cm ,那么点A 与⊙O 的位置关系是( A )
A .点A 在⊙O 外
B .点A 在⊙O 上
C .点A 在⊙O 内
D .不能确定
【解析】 ∵⊙O 的半径为5 cm ,OA =6 cm ,∴d >r ,∴点A 与⊙O 的位置关系是点A 在⊙O 外.
变式跟进
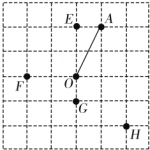
1.[2016·宜昌]在公园的O 处附近有E ,F ,G ,H 四棵树,位置如图1所示(图中小正方形的边长均相等).现计划修建一座以O 为圆心,OA 为半径的圆形水池,要求池中不留树木,则E ,F ,G ,H 四棵树中需要被移除的为( A )
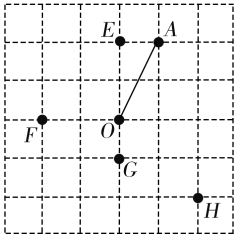
图1
A .E ,F ,G
B .F ,G ,H
C .G ,H ,E
D .H ,E ,F
【解析】 ∵OA =1+22=5,∴OE =2<OA ,∴点E 在⊙O 内;OF =2<OA ,∴点F 在⊙O 内;OG =1<OA ,∴点G 在⊙O 内;OH =22+22=22>OA ,∴点H 在⊙O 外.
题型二 垂径定理及其推论
例 2 如图2,⊙O 的直径CD =10,弦AB =8,AB ⊥CD ,垂足为M ,则DM 的长为( D )
A .5
B .6
C .7
D .
8
图2 例2答图
【解析】 连结OA ,如答图所示.
∵⊙O 的直径CD =10,∴OA =5,
∵弦AB =8,AB ⊥CD ,∴AM =12AB =12
×8=4, 在Rt △AOM 中,OM =OA 2-AM 2 =52-42=3,
∴DM =OD +OM =5+3=8.
【点悟】 已知直径与弦垂直的问题中,常连半径构造直角三角形,其中斜边为圆的半径,两直角边是弦长的一半和圆心到弦的距离,从而运用勾股定理来计算.
变式跟进
2.如图3,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,若CD =8,且AE ∶BE =1∶4,则AB 的长度为( A )
A .10
B .5
C .12
D.53
图3 第2题答图 【解析】 如答图,连结OC ,设AE =x ,∵AE ∶BE =1∶4,∴BE =4x ,∴OC =2.5x ,∴OE =1.5x ,∵CD ⊥AB ,∴CE =DE =12
CD =4,Rt △OCE 中,OE 2+CE 2=OC 2,∴(1.5x )2+42=(2.5x )2,∴x =2,∴AB =10.
3.有一座弧形的拱桥如图4,桥下水面的宽度AB 为7.2 m ,拱顶与水面的距离CD 的长为2.4 m ,现有一艘宽3 m ,船舱顶部为长方形并且高出水面2 m 的货船要经过这里,此货船能顺利通过这座拱桥吗?
图4 第3题答图
解:如答图,连结ON ,OB .
∵OC ⊥AB ,∴D 为AB 中点,
∵AB =7.2 m ,∴BD =12
AB =3.6 m. 又∵CD =2.4 m ,
∴设OB =OC =ON =r ,则OD =(r -2.4)m.
在Rt △BOD 中,由勾股定理得r 2=(r -2.4)2+3.62,解得r =3.9.
∵CD =2.4 m ,船舱顶部为长方形并高出水面2 m ,∴CE =2.4-2=0.4(m),
∴OE =r -CE =3.9-0.4=3.5(m),
在Rt △OEN 中,EN 2=ON 2-OE 2=3.92-3.52=2.96(m 2),∴EN ≈1.72(m).
∴MN =2EN =2×1.72=3.44 m >3,
∴此货船能顺利通过这座弧形拱桥.
题型三 圆周角定理的综合
例 3 [2017·市南区一模]如图5,在直径为AB 的⊙O 中,C ,D 是⊙O 上的两点,∠AOD =58°,CD ∥AB ,则∠ABC 的度数为__61°__.
图5
【解析】 ∵∠AOD =58°,∴∠ACD =∠AOD =29°,∵CD ∥AB ,∴∠CAB =∠ACD =29°,∵AB 是直径,∴∠ACB =90°,∴∠ABC =90°-29°=61°.
【点悟】 (1)在同圆(或等圆)中,圆心角(或圆周角)、弧、弦中只要有一组量相等,则其他对应的各组量也分别相等,利用这个性质可以将问题互相转化,达到求解或证明的目的;(2)注意圆中的隐含条件(半径相等)的应用;(3)圆周角定理及其推论,是进行圆内角度数转化与计算的主要依据,遇直径,要想到直径所对的圆周角是90°,从而获得到直角三角形;遇到弧所对的圆周角与圆心角,要想到同弧所对的圆心角等于圆周角的2倍以及同弧所对的圆周角相等.
变式跟进
4.如图6,⊙O 是正方形ABCD 的外接圆,点P 在⊙O 上,则∠APB =__45°__.
图6 第4题答图 【解析】 如答图,连结OA ,OB .根据正方形的性质,得∠AOB =90°.再根据圆周角定理,得∠APB =45°.
5.[2017·永嘉二模]如图7,已知AB 是半圆O 的直径,OC ⊥AB 交半圆于点C ,D 是射线OC 上一点,连结AD 交半圆O 于点E ,连结BE ,CE .
(1)求证:EC 平分∠BED ;
(2)当EB =ED 时,求证:AE =CE.
图7 第5题答图
证明:(1)∵AB 是半圆O 的直径,∴∠AEB =90°,
∴∠DEB =90°.∵OC ⊥AB ,
∴∠AOC =∠BOC =90°,∴∠BEC =45°,
∴∠DEC =45°.∴∠BEC =∠DEC ,
即EC 平分∠BED ;
(2)如答图,连结BC ,OE ,
在△BEC 与△DEC 中,⎩⎪⎨⎪⎧BE =DE ,∠BEC =∠DEC ,EC =EC ,
∴△BEC ≌△DEC ,∴∠CBE =∠CDE .
∵∠CDE =90°-∠A =∠ABE ,∴∠ABE =∠CBE .
∴∠AOE =∠COE ,∴AE =CE .
题型四 弧长的计算
例 4 如图8,△ABC 是正三角形,曲线CDEF 叫做“正三角形的渐开线”,其中,CD ︵,DE ︵,EF ︵,圆心依次按A ,B ,C …循环,它们依次相连结.若AB =1,则曲线CDEF 的长是__4π__(结果保留π).
图8
【解析】 CD ︵的长是120π·1180=2π3,DE ︵的长是120π·2180=4π3,EF ︵的长是120π·3180=2π,则曲线CDEF 的长是23
π+43
π+2π=4π.
变式跟进
6.一个扇形的半径为8 cm ,弧长为163π cm ,则扇形的圆心角为__120°__. 【解析】 设扇形的圆心角为n °,根据题意得163π=n π×8180,解得n =120,∴扇形的圆心角为120°. 题型五 扇形的面积计算
例 5 [2016·河南]如图9,在扇形AOB 中,∠AOB =90°,以点A 为圆心,OA 的长为半径作OC ︵交AB ︵于点C ,若OA =2,则阴影部分的面积是 3-13π .
图9 例5答图 【解析】 如答图,连结OC ,AC ,△OAC 是等边三角形,扇形OBC 的圆心角是30°,阴影部分的面积等于扇形OBC 的面积减去弓形OC 的面积.S 扇形OBC =30π×22360=13π,S 弓形OC =60π×22360-34×22=23π-3,S 阴影=13π-⎝ ⎛⎭⎪⎫23π-3=3-13π. 【点悟】 求不规则图形的面积,常转化为易解决的基本图形,然后求出各图形的面积,通过面积的和差求出结果.
变式跟进
7.若扇形的半径为3 cm ,扇形的面积为2π cm 2,则该扇形的圆心角为__80__°,弧长为__43π__cm. 【解析】 由n π·32360=2π,解得n =80,由2π=12l ×3,解得l =43π.
8.如图10,以AB 为直径的⊙O 经过AC 的中点D ,DE ⊥BC 于点E ,若DE =1,∠C =30°,则图中阴影部分的面
积是 49π-33
图10
【解析】 ∵∠C =30°,DE =1,∠DEC =90°,∴DC =2,∵OD ∥BC ,∴∠ODA =30°,∵OD =OA ,∴∠OAD =
∠ODA =30°,∴∠AOD =120°,∴OA =233,∴S 阴影=120π×⎝ ⎛⎭⎪⎫2332360-12×2×33=49π-33
. 题型六 圆锥
例 6 [2017·西湖区校级三模]一个圆锥的侧面展开图是圆心角为120°且半径为6的扇形,则这个圆锥的底面半径为( B )
A .2
B .2
C .2.5
D .3
【解析】 设这个圆锥的底面半径为r ,根据题意,得2π·r =120π·6180,解得r =
2. 【点悟】 (1)圆锥侧面展开图是一个扇形;(2)圆锥的底面周长是其侧面展开图的弧长;(3)圆锥的母线就是其侧面展开扇形的半径.
变式跟进
9.一个圆锥的底面半径是5 cm ,其侧面展开图是圆心角为150°的扇形,则圆锥的母线长为( B )
A .9 cm
B .12 cm
C .15 cm
D .18 cm
【解析】 设圆锥的母线长为l ,根据题意得2π×5=150πl 180,解得l =12.即圆锥的母线长为12 cm.
过关训练
1.一个圆锥形的圣诞帽底面半径为12 cm ,母线长为13 cm ,则圣诞帽的侧面积为( B )
A .312π cm 2
B .156π cm 2
C .78π cm 2
D .60π cm 2
【解析】 圆锥的底面周长是12×2π=24π,则圆锥的侧面积是12×24π×13=156π(cm 2).
2.[2017·连云港三模]一个滑轮起重装置如图1所示,滑轮的半径是15 cm ,当重物上升15 cm 时,滑轮的一条半径OA 绕轴心O 按顺时针方向旋转的角度约为(π取3.14,结果精确到1°)( C )
图1
A .115°
B .60°
C .57°
D .29° 【解析】 根据题意得15=n π·15180,解得n =180°π
≈57°,∴OA 绕轴心O 按顺时针方向旋转的角度约为57°. 3.一个隧道的横截面如图2所示,它的形状是以点O 为圆心,5为半径的圆的一部分,M 是⊙O 中弦CD 的中点,EM 经过圆心O 交⊙O 于点E .若CD =6,则隧道的高(ME 的长)为( D )
图2
A .4
B .6
C .8
D .9
【解析】 ∵M 是⊙O 弦CD 的中点,根据垂径定理:EM ⊥CD ,又CD =6,则有CM =12CD =3,设OM 是x ,在Rt △COM 中,有OC 2=CM 2+OM 2,即52=32+x 2,解得x =4,∴EM =5+4=9.
4.[2017·大庆模拟]如图3是圆内接正方形ABCD ,分别将AB ︵,BC ︵,CD ︵,DA ︵沿边长AB ,BC ,CD ,DA 向内翻折,已知BD =2,则阴影部分的面积为__4-π__.
图3
【解析】 由圆内接正方形的性质知,正方形的边长等于半径的2倍,∴阴影部分的面积=(2)2-[π-(2)2]=4-π.
5.[2016·贵港]如图4,在Rt △ABC 中,∠C =90°,∠BAC =60°,将△ABC 绕点A 逆时针旋转60°后得到△ADE ,若AC =1,则线段BC 在上述旋转过程中扫过部分(阴影部分)的面积是__π2__(结果保留π).
图4
【解析】 ∵∠C =90°,∠BAC =60°,AC =1,∴AB =2,S 扇形BAD =60π·22360=2π3,S 扇形CAE =60π·12360=π6,则S 阴影=S 扇形DAB +S △ABC -S △ADE -S 扇形ACE =23π-π6=π2.
6.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图5所示,已知水杯的半径是4 cm ,水面宽度AB 是4 3 cm.
(1)求水的最大深度(即CD )是多少?
(2)求杯底有水部分的面积(阴影部分).
图5
解:(1)∵OD ⊥AB ,AB =4 3 cm ,
∴BC =12AB =12×43=23(cm), 在Rt △OBC 中,∵OB =4 cm ,BC =23(cm),
∴OC =OB 2-BC 2=42-(23)2
=2(cm),
∴DC =OD -OC =4-2=2(cm).
∴水的最大深度(即CD )是2 cm ;
(2)∵OC =2,OB =4,∴OC =12
OB , ∴∠ABO =30°,∵OA =OB ,
∴∠BAO =∠ABO =30°,∴∠AOB =120°,
∵S △AOB =12AB ·OC =12×43×2=43, S 扇形OAB =120π×42360=163π,
∴S 阴影=S 扇形-S △AOB =⎝ ⎛⎭
⎪⎫163π-43 cm 2.
7.[2017·苏州一模]如图6,已知Rt △ABD 中,∠A =90°,将斜边BD 绕点B 顺时针方向旋转至BC ,使BC ∥AD ,过点C 作CE ⊥BD 于点E .
(1)求证:△ABD ≌△ECB ;
(2)若∠ABD =30°,BE =3,求CD ︵的长.
图6
解:(1)证明:∵∠A =90°,CE ⊥BD ,
∴∠A =∠BEC =90°.
∵BC ∥AD ,∴∠ADB =∠EBC .
∵将斜边BD 绕点B 顺时针方向旋转至BC ,
∴BD =BC .在△ABD 和△ECB 中,
⎩⎪⎨⎪⎧∠ADB =∠EBC ,∠A =∠BEC ,BD =CB ,
∴△ABD ≌△ECB ;
(2)∵△ABD ≌△ECB ,∴AD =BE =3.
∵∠A =90°,∠ABD =30°,∴BD =2AD =6,
∵BC ∥AD ,∴∠A +∠ABC =180°,
∴∠ABC =90°,∴∠DBC =60°,
∴CD ︵的长为60π×6180
=2π. 8.[2017·高密模拟]如图7,AB 为圆O 的直径,CD ⊥AB 于点E ,交圆O 于点D ,OF ⊥AC 于点F .
(1)求证:OF =12
BD ; (2)当∠D =30°,BC =1时,求圆中阴影部分的面积.
图7 第8题答图
解:(1)证明:∵OF ⊥AC ,∴AF =FC ,
∵OA =OB ,∴BC =2OF ,∵AB ⊥CD ,
∴BC ︵=BD ︵,∴BC =BD ,∴OF =12
BD ; (2)如答图,连结OC ,则OC =OA =OB ,
∵∠D =30°,∴∠A =∠D =30°,
∴∠COB =2∠A =60°,∴∠AOC =120°,
∵AB 为⊙O 的直径,∴∠ACB =90°,
在Rt △ABC 中,BC =1,
∴AB =2,AC =3,∵OF ⊥AC ,
∴AF =CF ,∵OA =OB ,
∴OF 是△ABC 的中位线,∴OF =12BC =12,
∴S △AOC =12AC ·OF =12×3×12=34,
S 扇形AOC =13π×OA 2=π3,
∴S 阴影=S 扇形AOC -S △AOC =π3-34
9.[2017·河北区二模]如图8①,在Rt △ABC 中,∠ABC =90°,点M 是AC 的中点,以AB 为直径作⊙O 分别交AC ,BM 于点D ,E .
(1)求证:MD =ME ;
(2)如图②,连结OD ,OE ,当∠C =30°时,求证:四边形ODME 是菱形.
图8
证明:(1)在Rt △ABC 中,点M 是AC 的中点,
∴MA =MB ,∴∠A =∠MBA ,
∵四边形ABED 是圆内接四边形,
∴∠ADE +∠ABE =180°,
而∠ADE +∠MDE =180°,
∴∠MDE =∠MBA .同理可得∠MED =∠A ,
∴∠MDE =∠MED ,∴MD =ME ;
(2)∵∠C =30°,∴∠A =60°,
∴∠ABM =60°,∴△OAD 和△OBE 为等边三角形,
∴∠BOE =60°,∴∠BOE =∠A ,
∴OE ∥AC ,同理可得OD ∥BM ,
∴四边形DOEM 为平行四边形,而OD =OE ,
∴四边形ODME 是菱形.
10.[2017·东莞校级模拟]如图9,⊙O 的内接四边形ABCD 两组对边的延长线分别交于点E ,F .
(1)当∠E =∠F 时,则∠ADC =__90__°;
(2)当∠A =55°,∠E =30°时,求∠F 的度数;
(3)若∠E =α,∠F =β,且α≠β,请你用含有α,β的代数式表示∠A 的大小.
图9
解:(1)∵∠E =∠F ,∠DCE =∠BCF ,
∠ADC =∠E +∠DCE ,∠ABC =∠BCF +∠F ,
∴∠ADC =∠ABC ,
∵四边形ABCD 是⊙O 的内接四边形,
∴∠ADC +∠ABC =180°,
∴∠ADC =90°;
(2)∵在△ABE 中,∠A =55°,∠E =30°,
∴∠ABE =180°-∠A -∠E =95°,
∴∠ADF =180°-∠ABE =85°,
∴在△ADF 中,∠F =180°-∠ADF -∠A =40°;
(3)∵∠ADC =180°-∠A -∠F ,∠ABC =180°-∠A -∠E ,
又∵∠ADC +∠ABC =180°,
∴180°-∠A -∠F +180°-∠A -∠E =180°,
∴2∠A +∠E +∠F =180°,
∴∠A =90°-∠E +∠F 2=90°-α+β2
备注:以下内容仅显示部分,需完整版请下载!











